内容介绍

2024 LTspice电路仿真竞赛挑战题，包含有16道题，完成33、36、37、44题电路搭建及仿真以及实验报告。

注：受限于平台单个文件大小限制，完整实验报告见设计资源附件。完整视频见Bilibili主页视频合集。

挑战题35——温度测量与控制电路

实验介绍

已知铂电阻R_t的电阻值随温度t（°C）变化的关系为，。设计一个温度测量与控制电路，使温度稳定在85~100ºC。

设计步骤

1.电路图

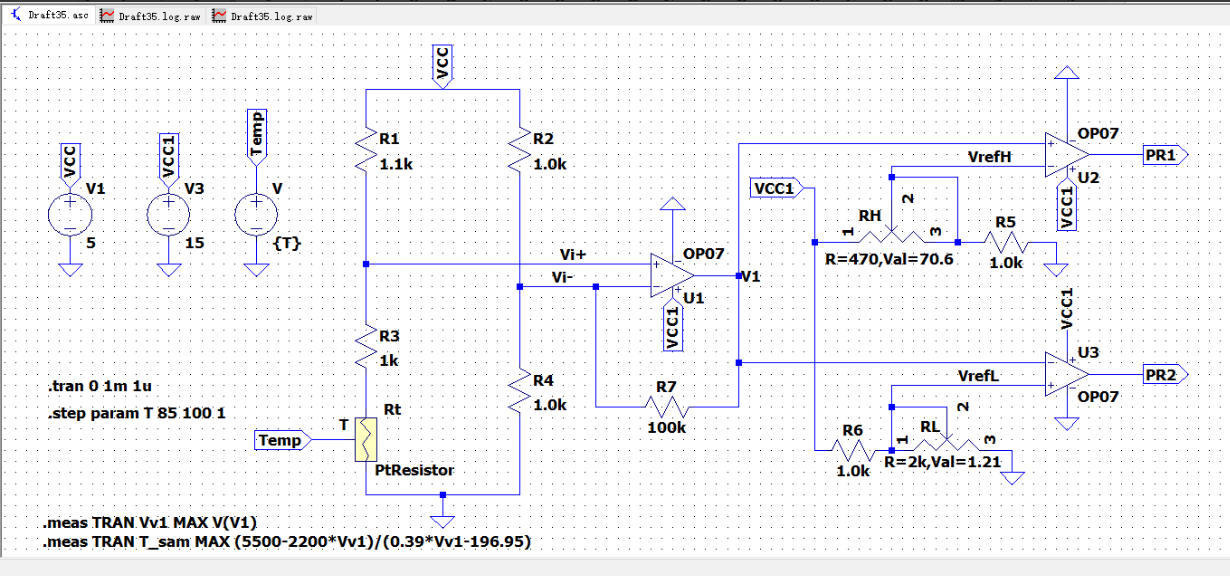
如下图，铂电阻Rt使用子电路封装，

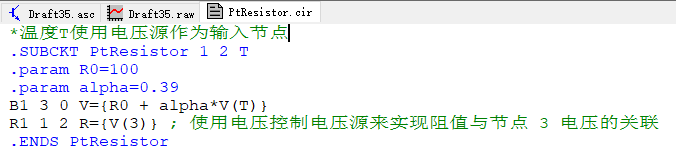
如下图，由三运放组成温度测量与控制电路（铂电阻PtResistor使用封装模型），使用桥式电路及运放U1组成差分放大电路（放大桥式电路的输出电压）；U2、U3均为电压比较器，分别与温度下限参考电压与温度上限参考电压作比较，并输出相应的高低电压。

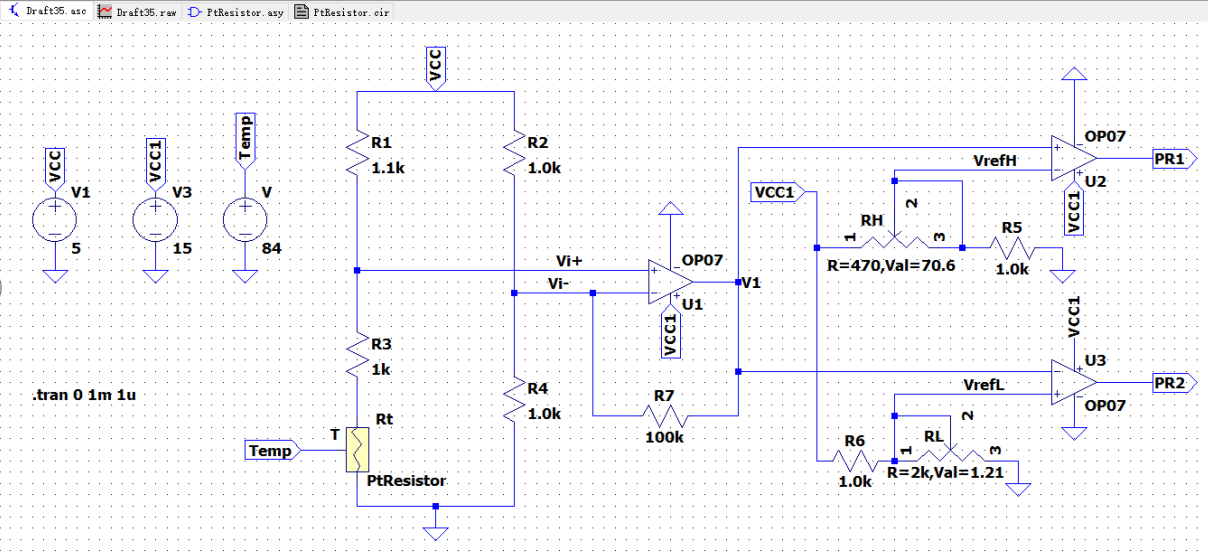
2.理论分析与计算

利用戴维南定理与叠加定理，对桥式电路采样电路进行等效，得到运放U1输出电压V1为：

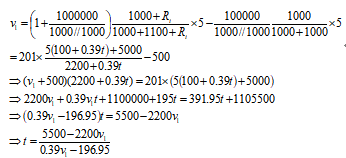
比较电路参数计算：

当t=85℃时，求得v1=9.9594；当t=100℃时，求得v1=11.2528；考虑运放供电电压经验值及设计余量，运放及比较电路工作电压Vcc为15V。

3.电路仿真

设置铂电阻温度为84℃＜85℃（下限温度），运行仿真，如下图，U2输出高电平（Vpr2=14.07V），U3输出低电平（Vpr2=930mV）

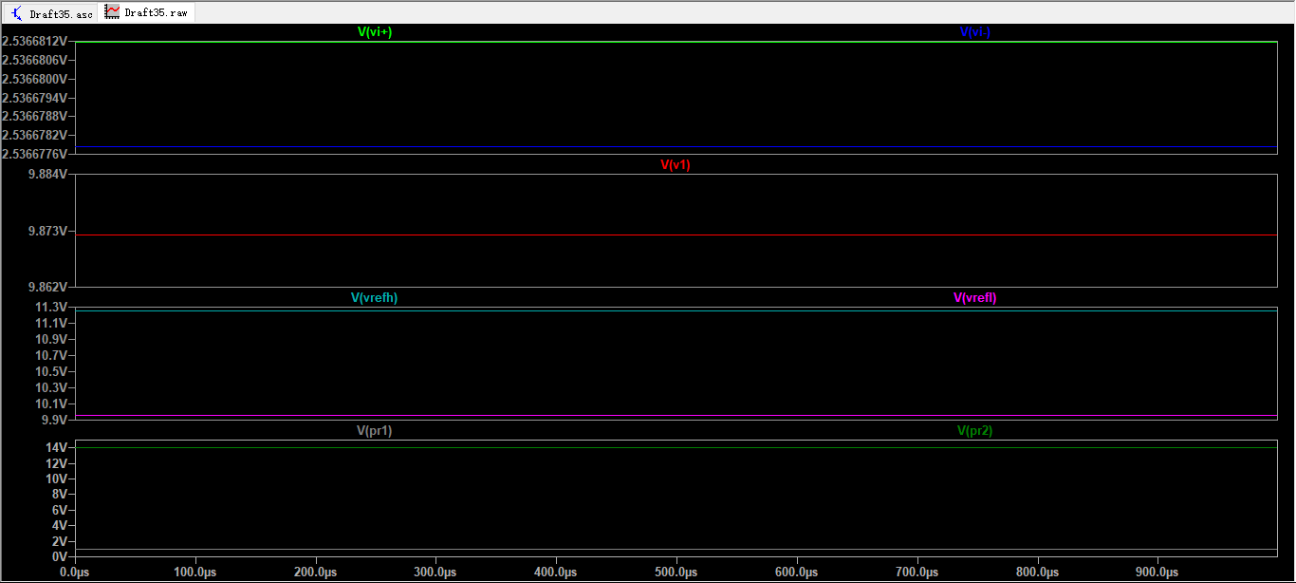
设置铂电阻温度为86℃＞85℃（下限温度），运行仿真，如下图，U2输出低电平（Vpr2=930mV），U3输出低电平（Vpr2=930mV）

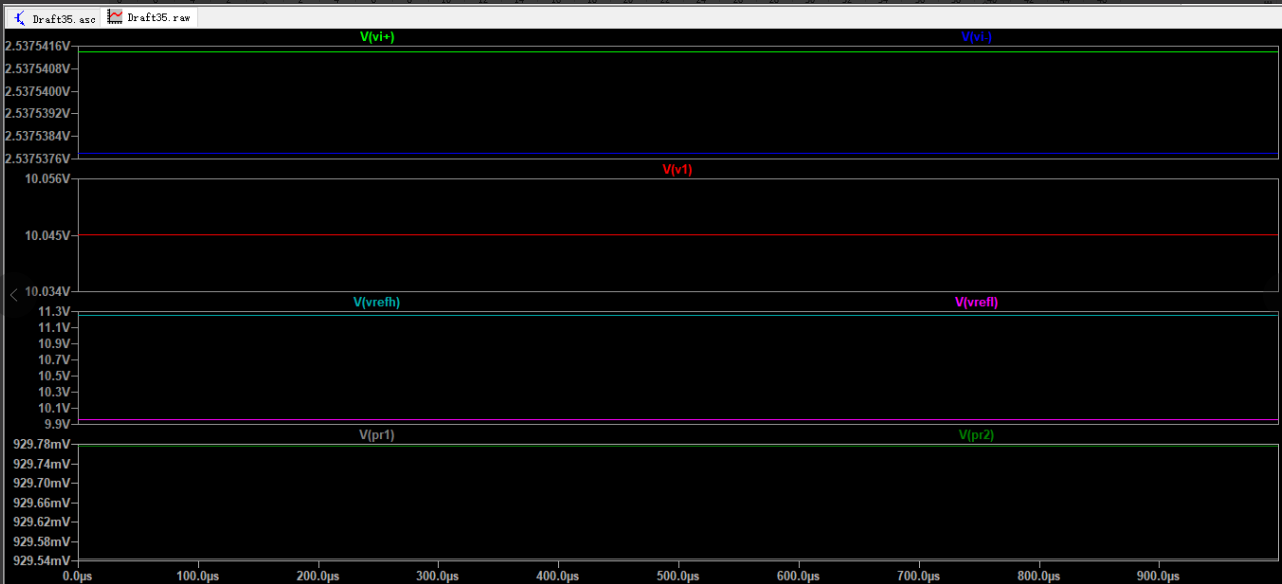
设置铂电阻温度为101℃＞100℃（上限温度），运行仿真，如下图，U2输出低电平（Vpr2=930mV），U3输出高电平（Vpr2=14.07mV）

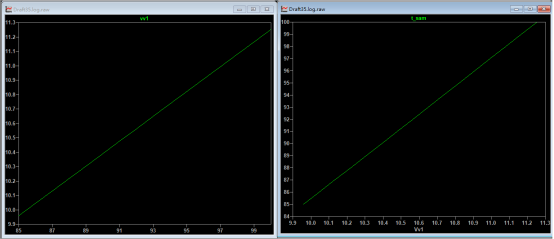
温度测量验证：对铂电阻温度T进行参数扫描，并记录运放U1输出电压V1即反算得到的采样温度值t_sam，如下图

Log文件数据记录如下：

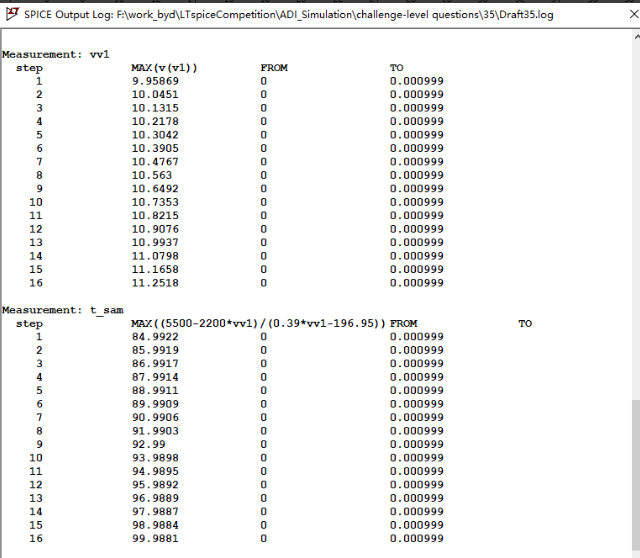
运放U1输出电压V1以及反算公式得到的采样温度值t_sam如下图

挑战题36——差分放大电路

实验介绍

设计一个差分放大电路，使它的CMRR＝95dB。

设计步骤

1.电路选型及搭建

如图1所示是基本的共射放大电路，其静态工作点基本稳定。但是温度的变化会使得集电极电流发生微小的变化，采用直接耦合的方式会进一步放大该变化，引起静态工作点的变化（温漂）。

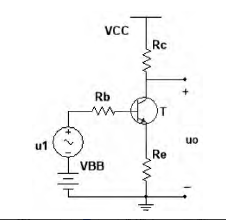
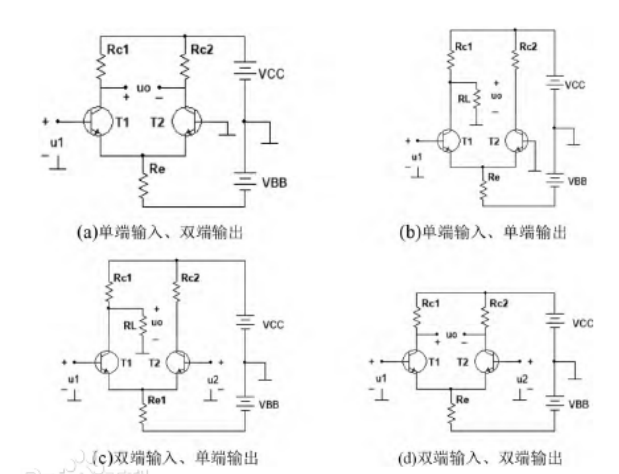
图2（d）中为典型的双端输入双端输出的差分放大电路，由于该放大电路两个晶体管射极电阻Re使共模抑制比较难达到95dB。

因此本题将电阻Re替换为恒流源电路，搭建电路如下图所示（chadong.asc）。

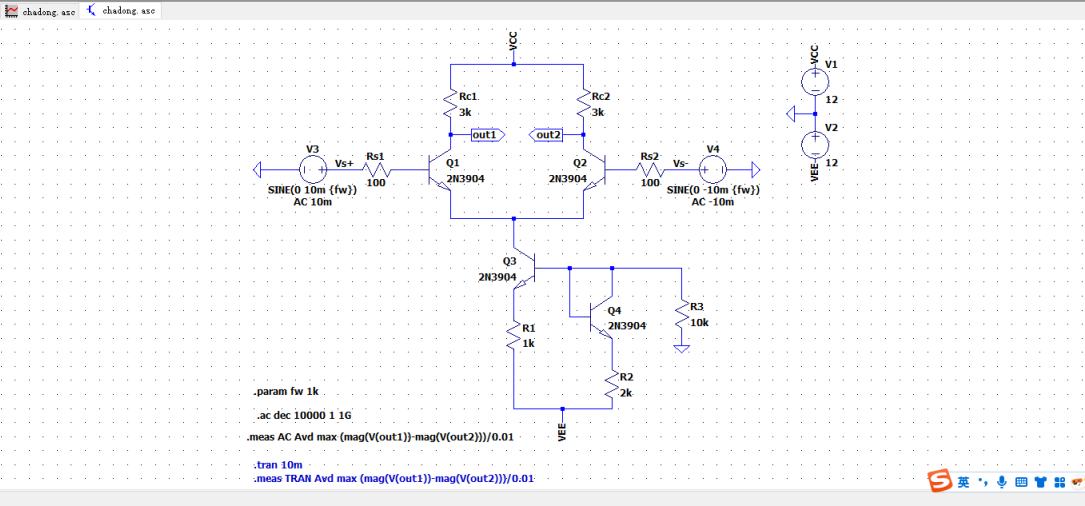
2.电路仿真

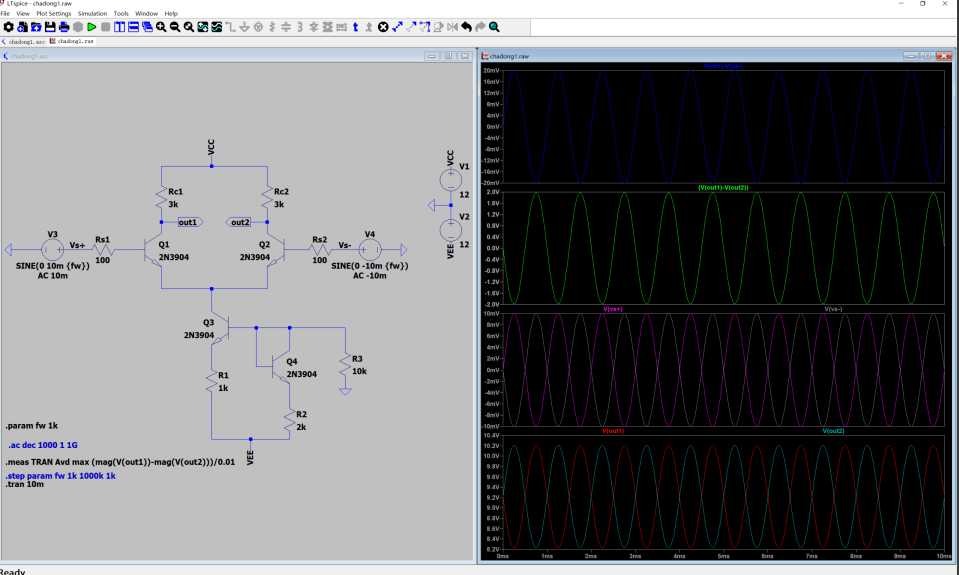
（1）如下图，对该差分放大器的两个输入端输入±10mV、1kHz的差分电压后。两个输出端out1、out2的输出差分电压幅值为2V，放大器增益为100。

（2）分析双端输入时的差模电增益

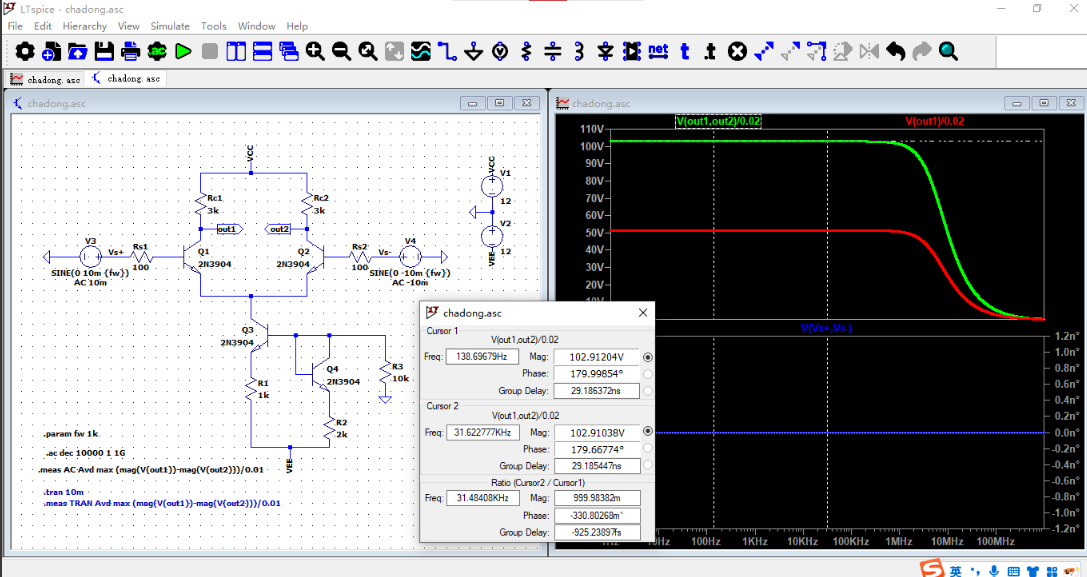
进行交流分析，两个差分输入端分别设置10mV和-10mV的AC电压，频率范围为1Hz~1GHz。

交流分析结果如下图所示，双端输入双端输出的差模电压增益为102.912（纵坐标以原始增益显示），双端输入单端输出的差模电压增益为51.455.

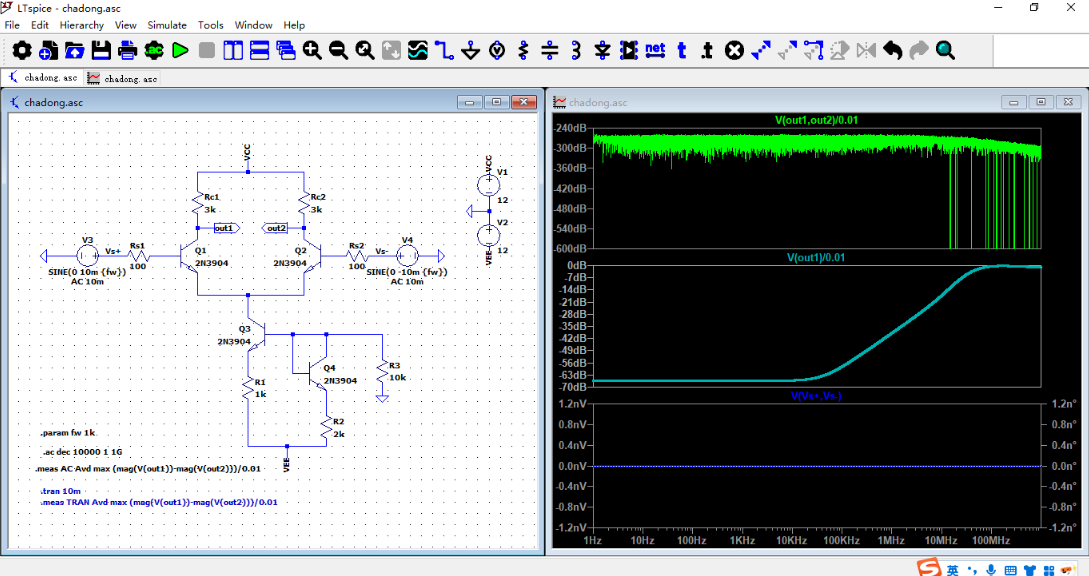
(3)分析双端输入时的共模电压增益

如下图进行交流分析，两个差分输入端均设置10mV的AC电压，频率范围为1Hz~1GHz。分析结果如下图所示，双端输入双端输出的共模电压增益为0（纵坐标以原始增益显示）。

（4）共模抑制比分析

封装差分放大电阻及子电路如左下图（chadong_sub.asc），搭建共模抑制比分析电路如由右下图（CMRR.asc）。

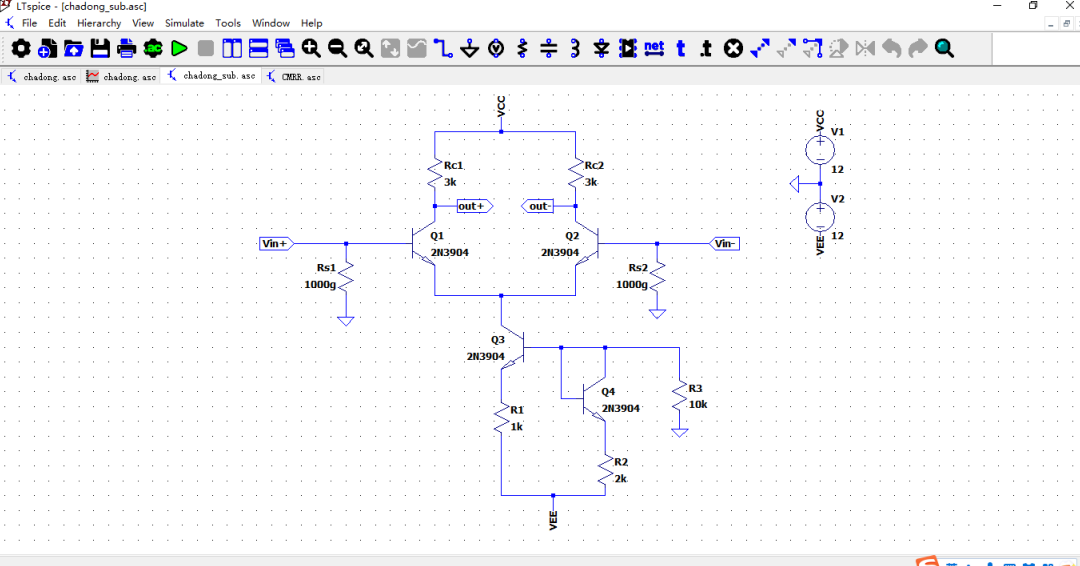
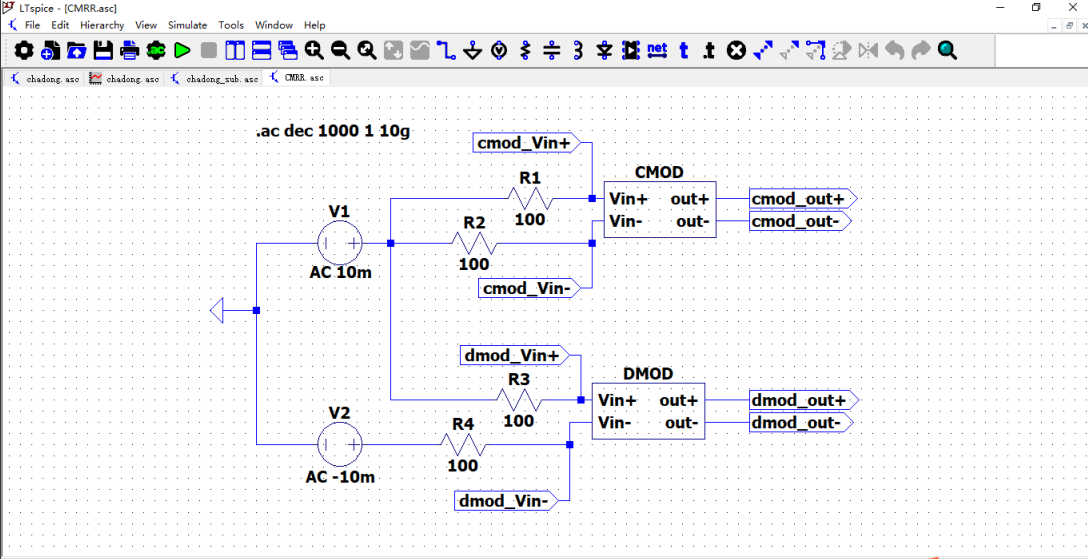
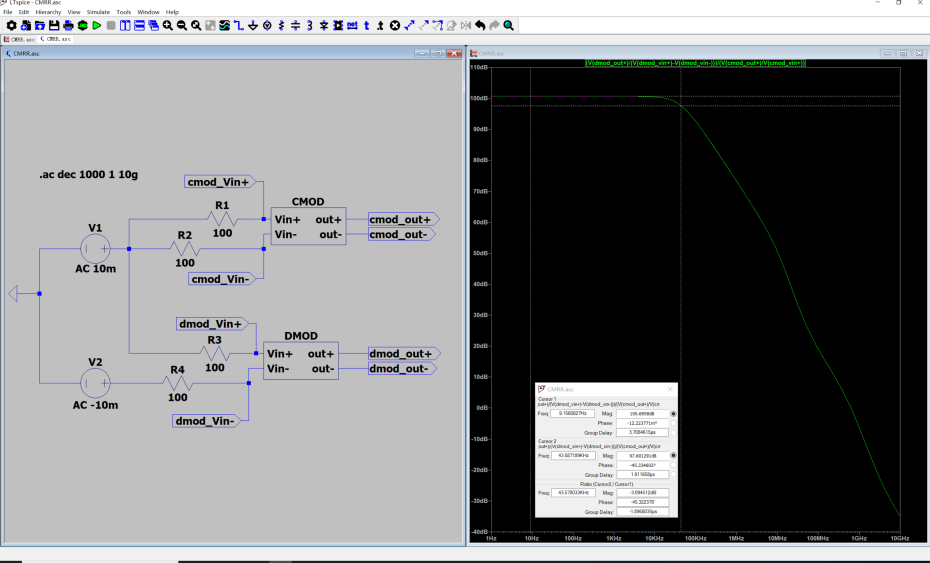
仿真结果如下，双端输入双端输出的共模抑制比为无穷大，双端输入单端输出的共模抑制比为100.69dB。大于题目要求的95dB。

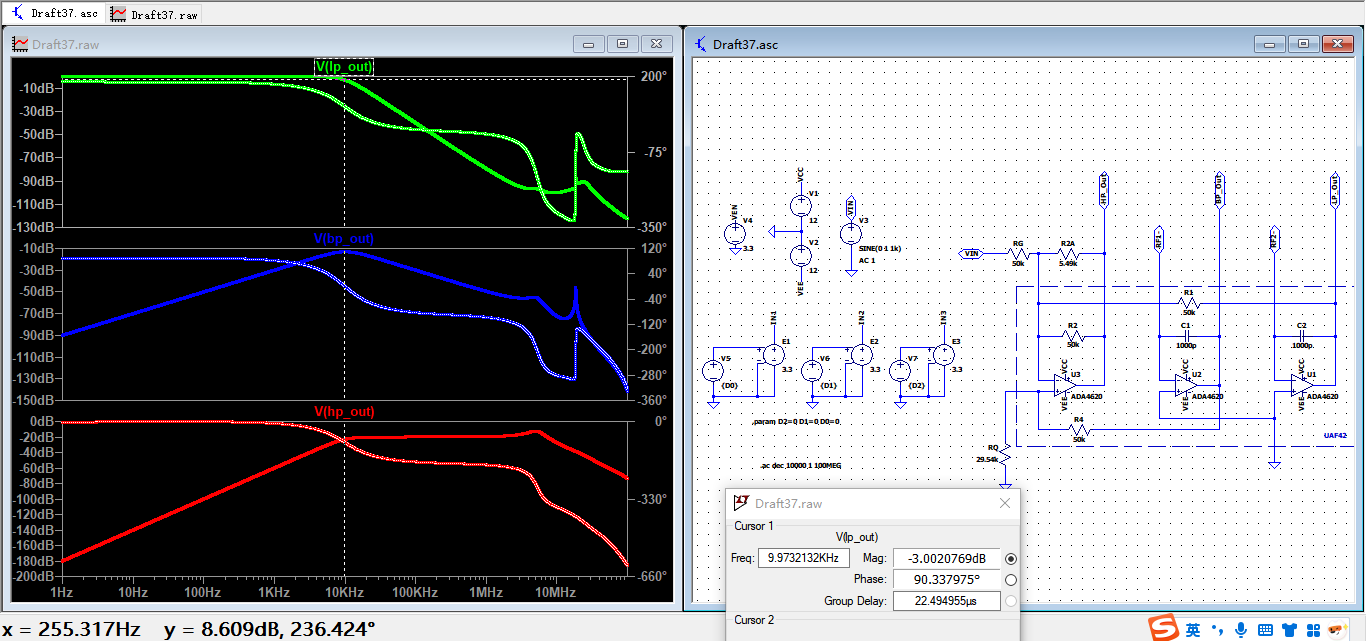
挑战题37——数控滤波器

实验介绍

利用状态变量型有源滤波器，设计一个数控有源滤波器。当控制端输入二进制数从000到111变化时，对应特征频率由1/8f变化到f。

设计步骤

1.电路选型及搭建

根据通用型有源滤波器如UAF42数据手册（UAF42 数据表、产品信息和支持 | 德州仪器 TI.com.cn），该滤波器可实现低通、高通、带通滤波。

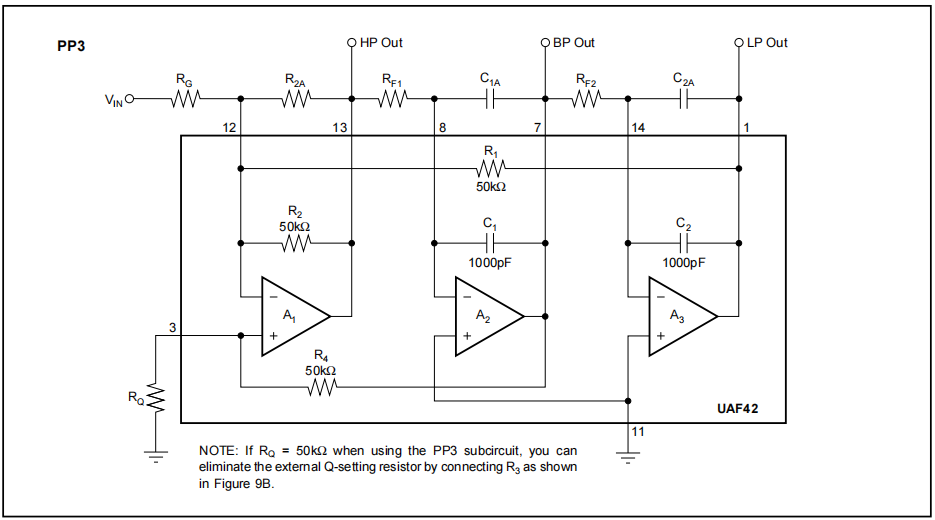
该滤波器反向极对点的内部原理图如左下图，

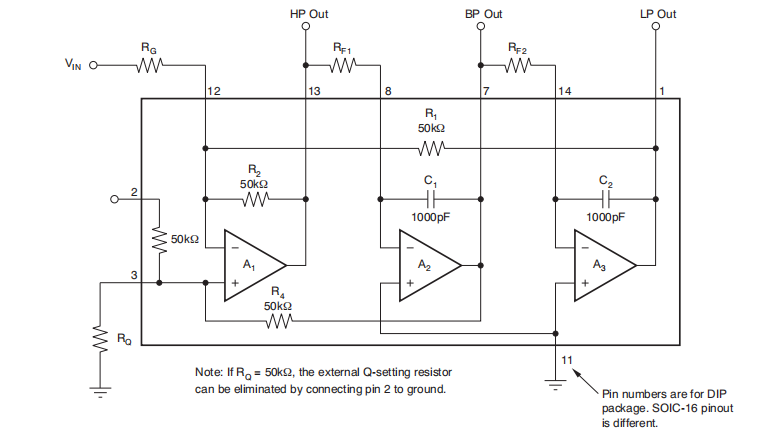
设计方程如右下图，

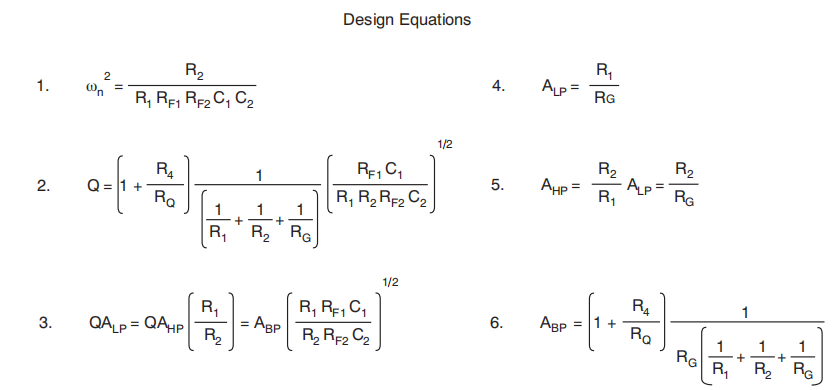
以巴特沃斯低通滤波器为例，传递函数为：

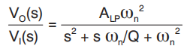
该仿真电路设计选型参考UAF42应用手册Figure 9a图（filter42/UAF42ApplicationBulletin.pdf at master · peterpolidoro/filter42 · GitHub），

使用MATLAB进行巴特沃斯低通滤波器参数设计流程如下：

（1）根据设计方程，计算得到特征频率由1/8f变化到f（f=10kHz）时，调整电阻RF2=RF1及RQ阻值如下

% 根据uaf42手册P7 Inverting Pole-Pair特征角频率ωn和品质因数，按照RG=50kΩ，RF1=RF2=RF,计算RF的值和RQ的值
% 根据uaf42通用有源滤波器设计手册P4,加入外部电阻R2A=5.49kΩ与内部R2并联
% 根据P6 PP3反向极点对子电路图以及设计方程计算RF和RQ的值。
% 根据uaf42通用有源滤波器设计手册P4建议PP3电路图中RG=50kΩ。
R1 = 50000;
R2 = 50000;
R2A = 5490;
R2 = R2*R2A/(R2+R2A);

R4 = 50000;
RG = 50000;
C1 = 1000*1e-12;
C2 = 1000*1e-12;
fc = [10000 20000 30000 40000 50000 60000 70000 80000];
wn = 2*pi*fc; % 根据图中 -3dB 频率为 10kHz 确定
RF1 = sqrt(R2./(R1*wn.^2*C1*C2))
RF2 = RF1;
Q = 1/sqrt(2);  % 巴特沃斯低通滤波器品质因数为sqrt(2)

syms RQ;
answ = solve((1+R4/RQ)*(1/(1/R1+1/R2+1/RG))*sqrt(RF1*C1/(R1*R2*RF1*C2))==Q,RQ)
RQ = double(answ)

计算得到8个特征频率下的滤波器频率调节电阻及调节品质因数的电阻RQ分别为：

RF1 = 1×8
103 ×
    5.0061    2.5030    1.6687    1.2515    1.0012    0.8343    0.7152    0.6258

RQ = 2.9535e+04

根据计算得到的RQ和其余电路参数计算二阶低通滤波器传递函数的系数，绘制该滤波器伯德图验证特征频率：

%% 根据传递函数画出伯德图
ALP = R1/RG;
AHP = R2/RG;
ABP = (1+R4/RQ)*(1/(RG*(1/R1+1/R2+1/RG)))

% 构建二阶巴特沃斯低通滤波器传递函数
num = [0 0 ALP*wn^2];
den = [1 wn/Q wn^2];
sys = tf(num, den);

% 设置频率范围
f_start = 10;
f_end = 1000*1000;
f = logspace(log10(f_start), log10(f_end), 1000);
w = 2*pi*f;

[mag, phase] = bode(sys, w);
mag = 20*log10(squeeze(mag)); % 转换为dB
phase = squeeze(phase-180);

% 绘制伯德图
subplot(2,1,1);
semilogx(f, mag);
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title('二阶巴特沃斯低通滤波器伯德图');
grid on;

subplot(2,1,2);
semilogx(f, phase);
xlabel('Frequency (Hz)');
ylabel('Phase (deg)');
grid on;

% 设置横坐标刻度和标签
xlim([f_start, f_end]); % 设置横坐标范围

得到f=10kHz时的伯德图如下图，特征频率为10kHz。

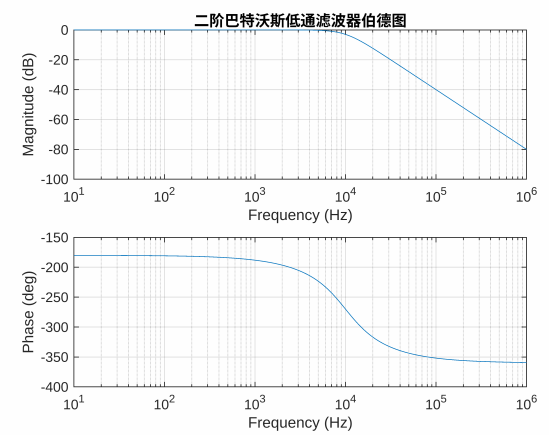
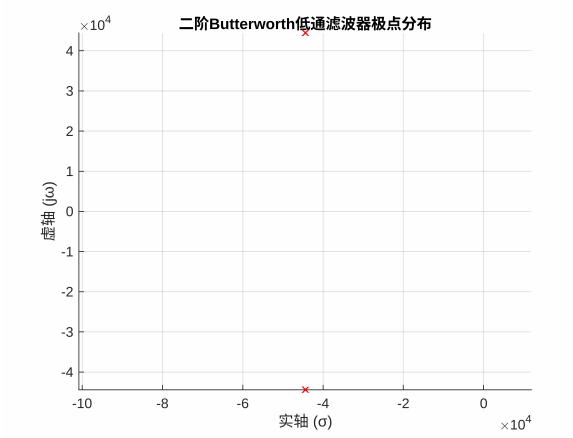
绘制该巴特沃斯低通滤波器极点分布，

根据 $H_{s} = \frac{ω _{n} ^{2}}{s ^{2} + ( \frac{ω _{n}}{Q} ) s + ω _{n} ^{2}}$ ，令分母等于0，得到极点为 $s = - \frac{ω _{n}}{2 Q} \pm j ω_{n} 1 - \frac{1}{4 Q ^{2}}$

% 二阶Butterworth低通滤波器极点绘制
% 令二阶低通滤波器传递函数分母等于0，解方程求解s
% 计算极点
Q = 1/sqrt(2); % Butterworth Q值
sigma = -wn/(2*Q); % 实部
omega = wn * sqrt(1 - 1/(4*Q^2)); % 虚部
poles = [sigma + 1j*omega, sigma - 1j*omega]; % 极点对

% 绘制极点图
figure;
scatter(real(poles), imag(poles), 'rx', 'LineWidth', 2);
hold on;
scatter(real(poles), -imag(poles), 'rx', 'LineWidth', 2); % 共轭极点
grid on;
xlabel('实轴 (σ)');
ylabel('虚轴 (jω)');
title('二阶Butterworth低通滤波器极点分布');
axis equal;

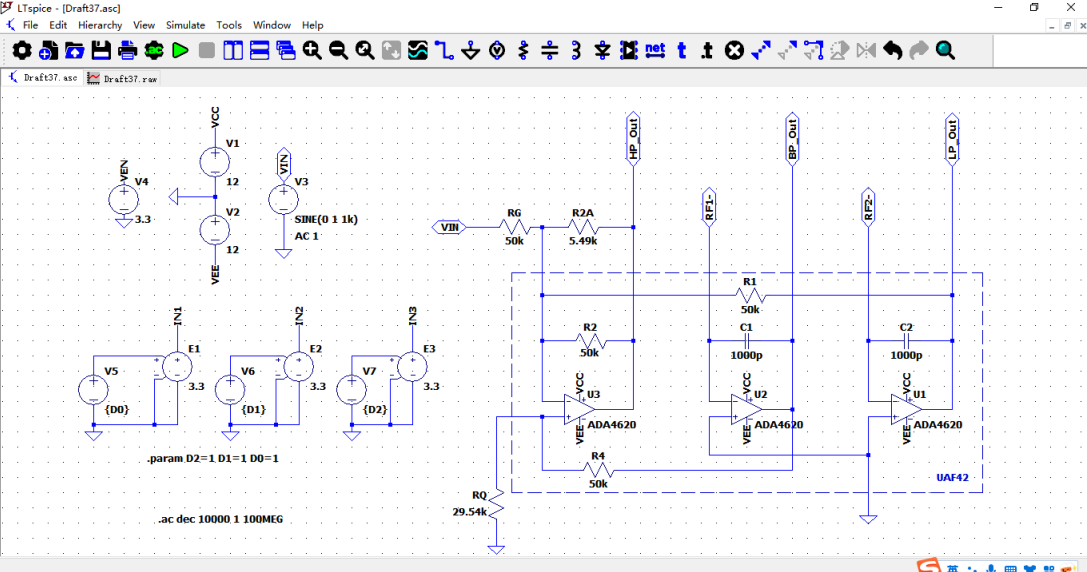
2.根据UAF42应用手册Figure 9a图及设计参数，电路搭建如下图，

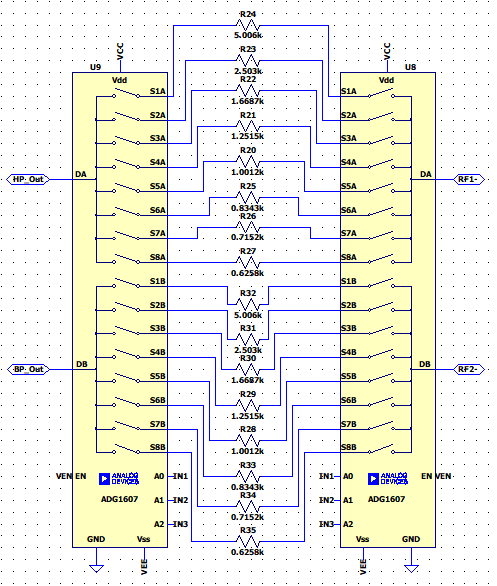
为实现该数控有源滤波器，且当控制端输入二进制数从000到111变化时，对应特征频率由1/8f变化到f。利用多路复用器以及MATLAB设计的RF1、RF2参数搭建如下数控电路，该电路根据A0、A1、A2控制端口状态选择RF1、RF2阻值，控制滤波器的截止频率。

仿真结果如下，当控制输入为111时，输出截止频率为80kHz（f=10kHz）。其余控制状态也可实现精确数字控制。

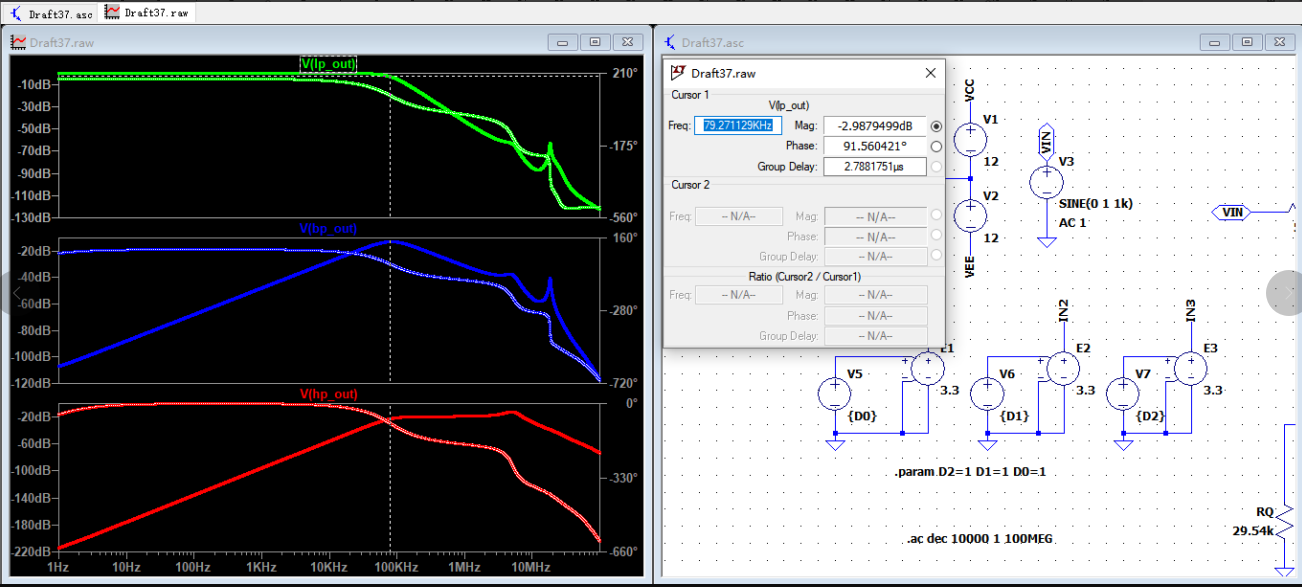
当控制输入为000时，特征频率为10kHz。