内容介绍

项目介绍

本项目背景是2024艾迈斯欧司朗dToF传感器光电设计竞赛，使用硬禾提供的dToF定制模块，完成给出的任务。
本项目使用dToF传感器为主体，使用ART-Pi板卡驱动,测算出传感器距离屏幕的夹角和垂直最小距离.

硬件说明

上图为tmf8821 dToF模块，集小型、高灵敏、准确与一体的传感器模块。

上图为ART-Pi开发板，是 RT-Thread 团队推出的高性能开源硬件开发板，专为嵌入式开发者及 DIY 爱好者设计，支持灵活扩展和多样化应用。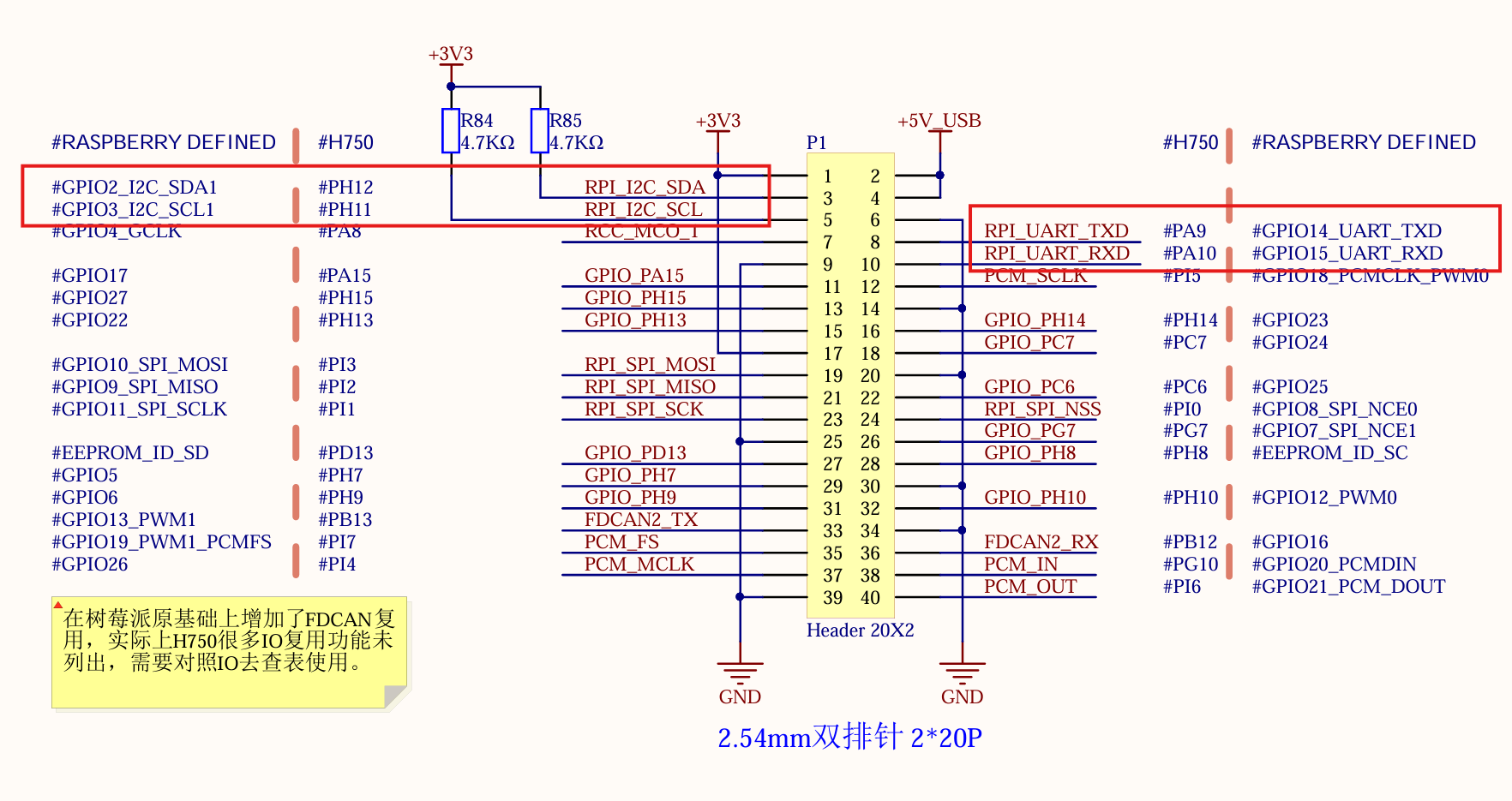

上图为连接的引脚,分别是SCL(H12)、SDA(H11)、INT(A9)、ENA(A10)。

方案说明

该传感器使用I2C即可完成配置和数据读取，因此可以使用任何带I2C接口的单片机或者SOC驱动。我因使用习惯选择了ART-Pi+rt-thread studio开发。
传感器工作模式我选择了3x3 Normal mode，9点作为原始数据。简单的做法可以以光学中心作为空间原点，分为X、Y两个方向单独做两次余弦定理算出平面夹角，然后以夹角算出距离。
但上述做法只使用了十字相交数据，当平面不在XY方向运动时就会测不出平面变化，经群里大佬解答，尝试使最小二乘法做平面拟合。

软件说明

驱动部分

软件I2C总线使用RTT标准驱动框架，然后跟着这位大佬分享的教程走TMF8821AM编程笔记。从上电到拿到测量数据基本能够走通，但是在官方资料中有说明，进行校准后可以得到更加准确的数据。具体参考自TMF882X_Host_Driver_Communication_AN001015_6中的4.4 Factory Calibration 。
其中的校准流程主要为开始校准->拿到校准参数 -> 写入参数-> 保存参数。至此完成校准。
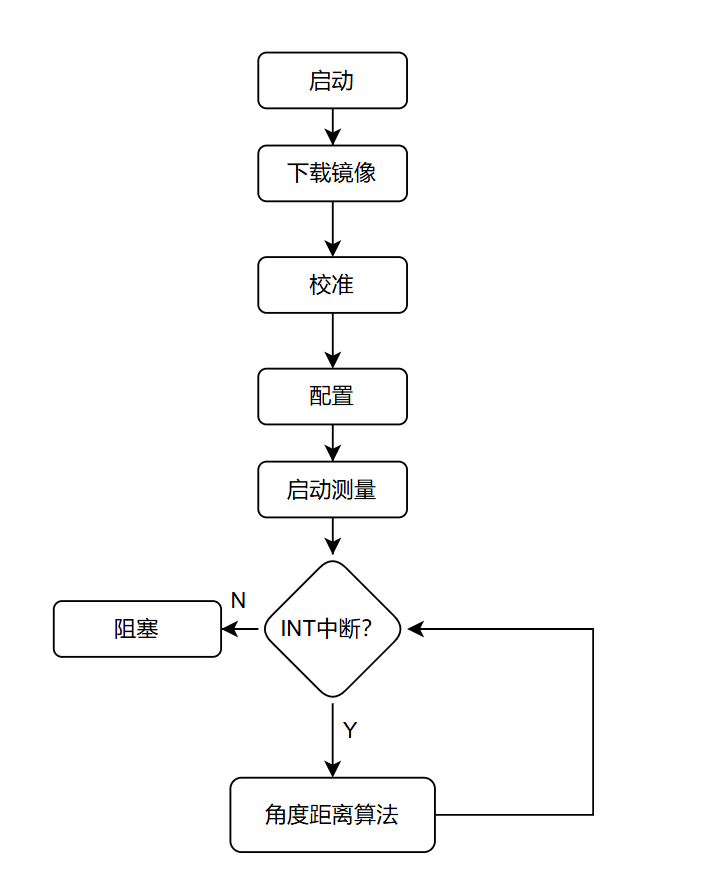
手册中提到关于一帧数据采集完成会拉低INT脚，因此我使用GPIO下降沿中断+释放信号量的方式来完成RTOS中的数据获取

算法部分

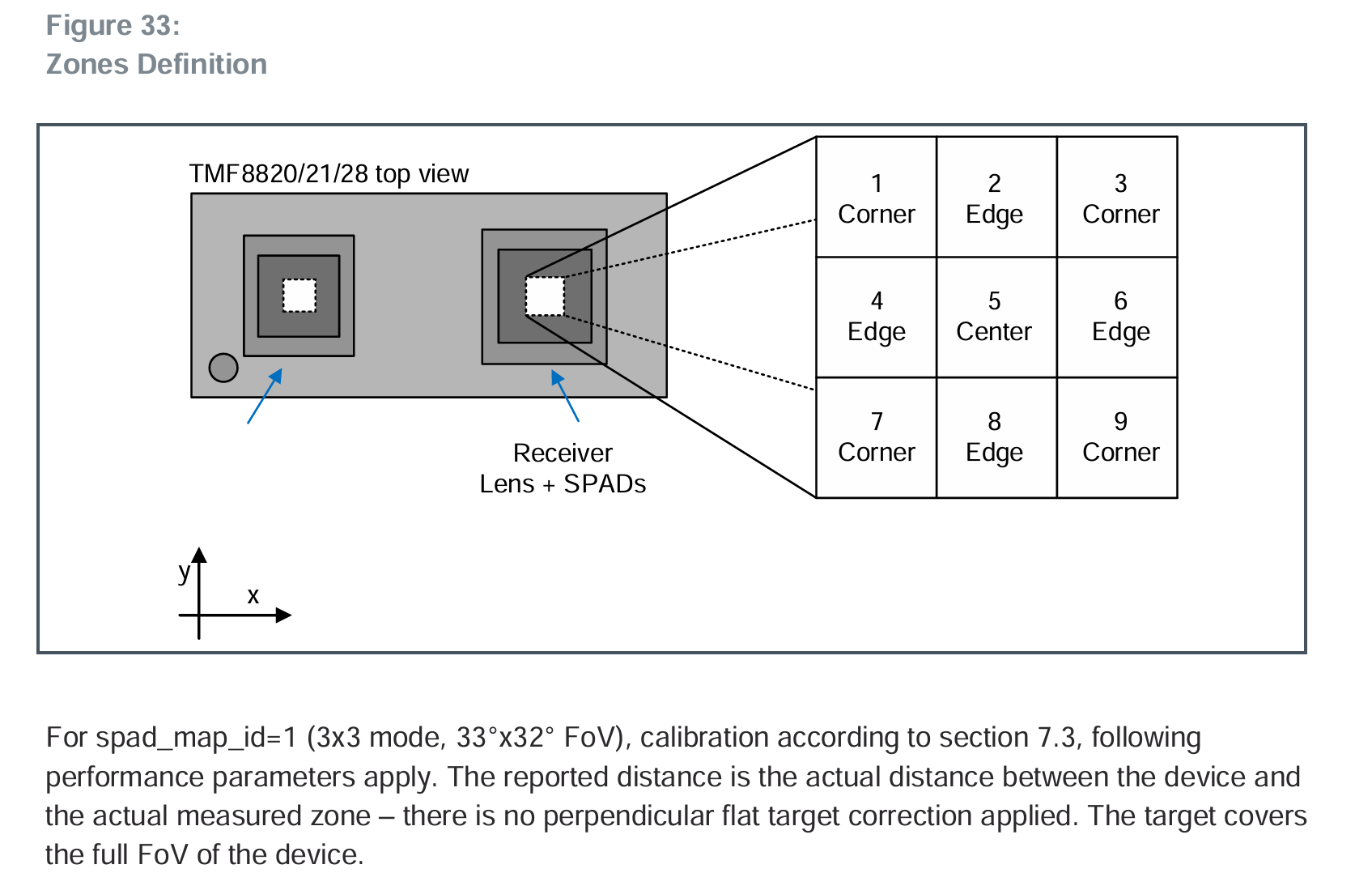
上图为spad_map_id = 1时的pads分布，可以清晰的看到其排列方式。

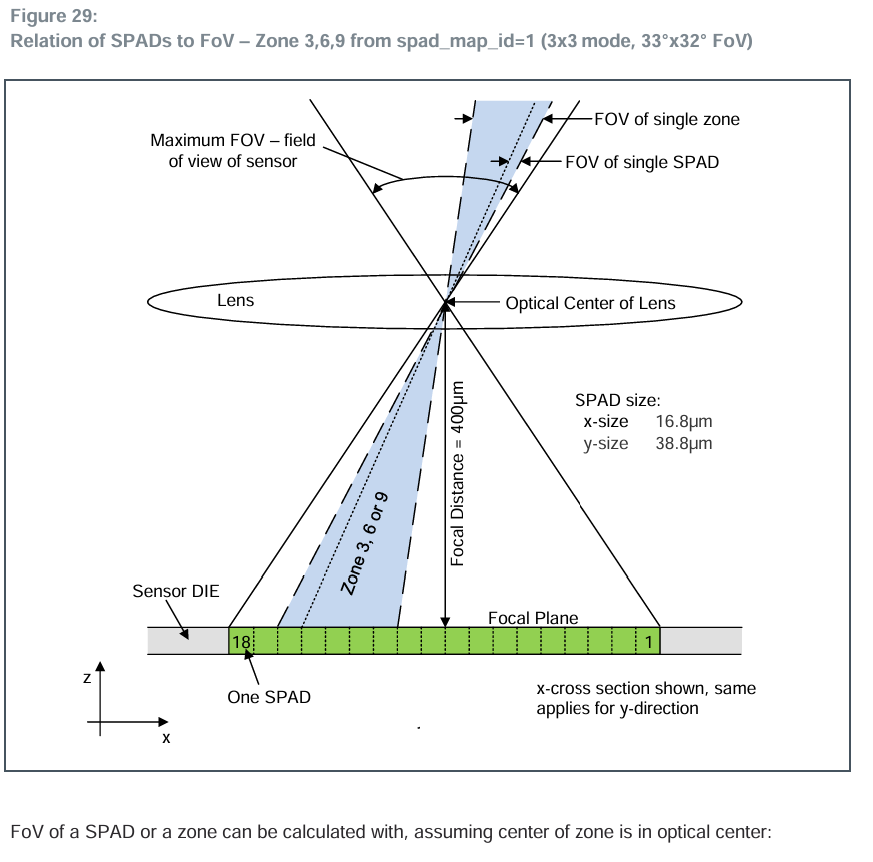
上图为实际的SPAD之间排列和结构。

上图为计算SPAD角度的计算公式。后面的算法主要根据这三张图来进行。

方法一：余弦定理

c2=a2+b2−2abcos⁡θc2=a2+b2−2abcosθ

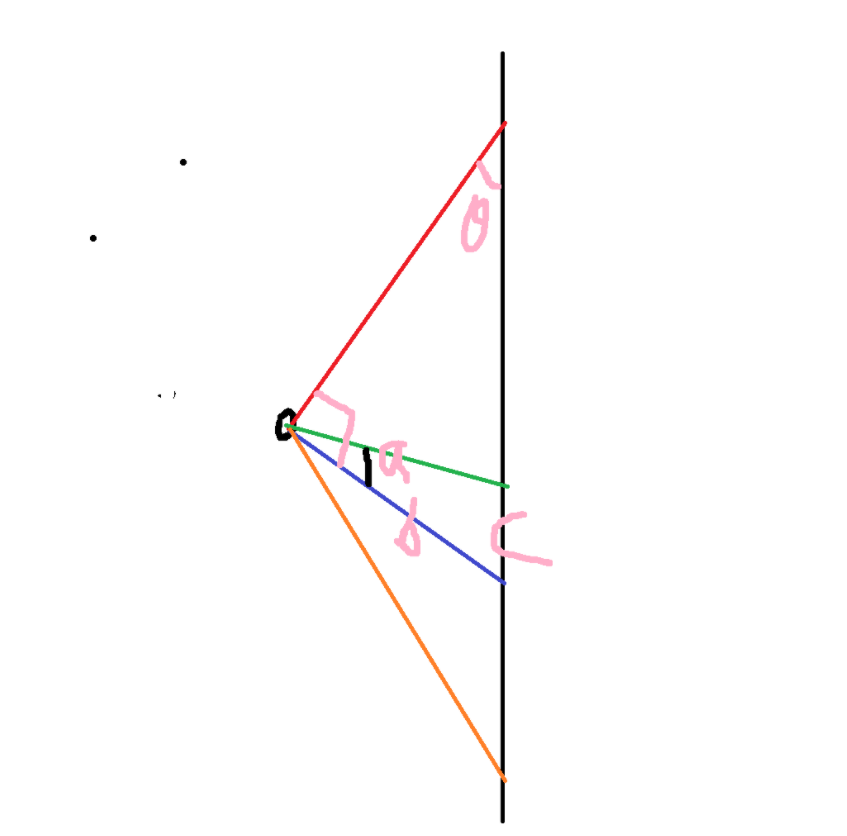
上图中的黑圈表示我们的传感器，线段a、b都是可以直接从原始数据中拿到的，角c也是已知的（可定为16度），这样就能用余弦定理算出c的长度，然后再用一次余弦定理就能算出角a，即求出平面夹角。

实现代码如下：

static double calculate_angel_distance(double a,double b,double angel_c)
{
    double c_rad=PI*angel_c/180.0f;
    double c= a*a+b*b-2*a*b*cos(c_rad);
    c=sqrt(c);
    double cos_A=(b*b+c*c-a*a)/(2*b*c);
    cos_A =MAX(-1,MIN(cos_A,1));
    double a_rad=acos(cos_A)* (180.0 / PI);
    return a_rad;
}

方法二：最小二乘法

引用维基百科中的定义：最小二乘法（英语：least squares method），又称最小平方法，是一种数学优化建模方法。它通过最小化误差的平方和寻找数据的最佳函数匹配。
我们可以定义最小二乘平面拟合函数z=ax+by+c ，参考自最小二乘线性及平面拟合原理及C++实现。直接将9个点的空间坐标带入其中，最后算出a、b、c ,得到平面方程，再使用法向量算出pitch角、roll脚以及距离。

实现代码如下：

// 最小二乘平面拟合函数    z=ax+by+c
int gFittingPlane(double *x, double *y, double *z, int n,
                  double *a, double *b, double *c) {
    if (n < 3) {
        rt_kprintf("error----\n");
        return -1;
    }

    double sum_x = 0.0, sum_y = 0.0, sum_z = 0.0;
    double sum_x2 = 0.0, sum_y2 = 0.0, sum_z2 = 0.0;
    double sum_xy = 0.0, sum_xz = 0.0, sum_yz = 0.0;

    // 计算累加和
    for (int i = 0; i < n; ++i) {
        sum_x += x[i];
        sum_y += y[i];
        sum_z += z[i];

        sum_x2 += x[i] * x[i];
        sum_y2 += y[i] * y[i];
//        sum_z2 += z[i] * z[i];

        sum_xy += x[i] * y[i];
        sum_xz += x[i] * z[i];
        sum_yz += y[i] * z[i];
    }

    // 构建系数矩阵
    double coeff[3][3] = {
        {sum_x2, sum_xy, sum_x},
        {sum_xy, sum_y2, sum_y},
        {sum_x, sum_y, n}
    };

    //xz, xy, x1, yz, y2, y1, z1, y1, n
    double matrix_a[3][3] = {
        {sum_xz, sum_xy, sum_x},
        {sum_yz, sum_y2, sum_y},
        {sum_z, sum_y, n}
    };
    //x2, xz, x1, xy, yz, y1, x1, z1, n)
    double matrix_b[3][3] = {
        {sum_x2, sum_xz, sum_x},
        {sum_xy, sum_yz, sum_y},
        {sum_x, sum_z, n}
    };
    //x2, xy, xz, xy, y2, yz, x1, y1, z1
    double matrix_c[3][3] = {
        {sum_x2, sum_xy, sum_xz},
        {sum_xy, sum_y2, sum_yz},
        {sum_x, sum_y, sum_z}
    };

    // 计算行列式
    double det = gDeterm3(coeff);
    det =det>0?det:-det;
    rt_kprintf("det=%d\n",(uint32_t)(det*1000));
    // 判断奇异性
    if (fabs(det) < EPSILON) {
        rt_kprintf("erro->\n");
        return -1;
    }
    // 计算a的分子行列式
    *a = gDeterm3(matrix_a) / det;
    // 计算b的分子行列式
    *b = gDeterm3(matrix_b) / det;
    // 计算c的分子行列式
    *c = gDeterm3(matrix_c) / det;
    return 0;
}

运行

编译&下载

编译完成后，将开发板的 ST-Link USB 口与 PC 机连接，然后将固件下载至开发板。

运行效果

上电后，日志如图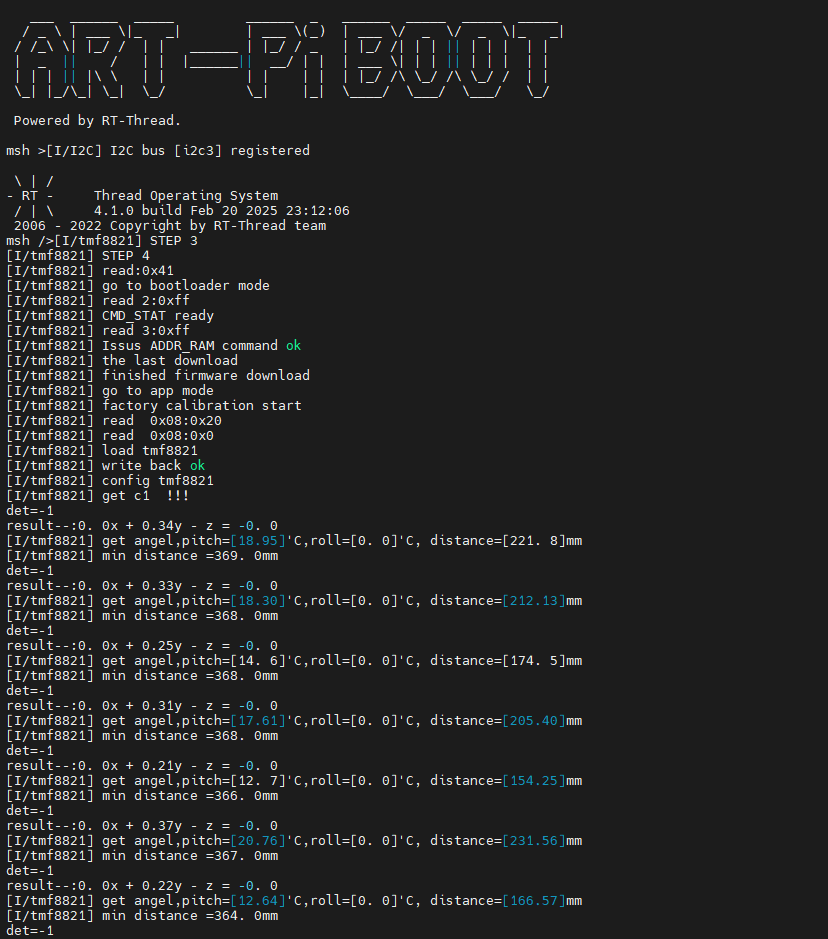

使用余弦定理计算如图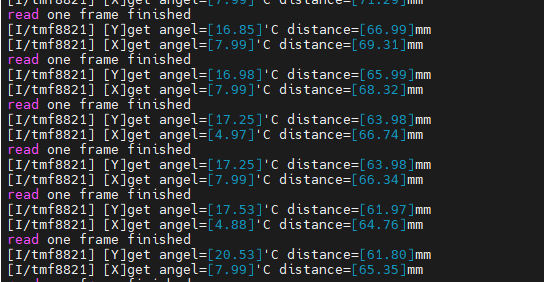

使用最小二乘法计算如图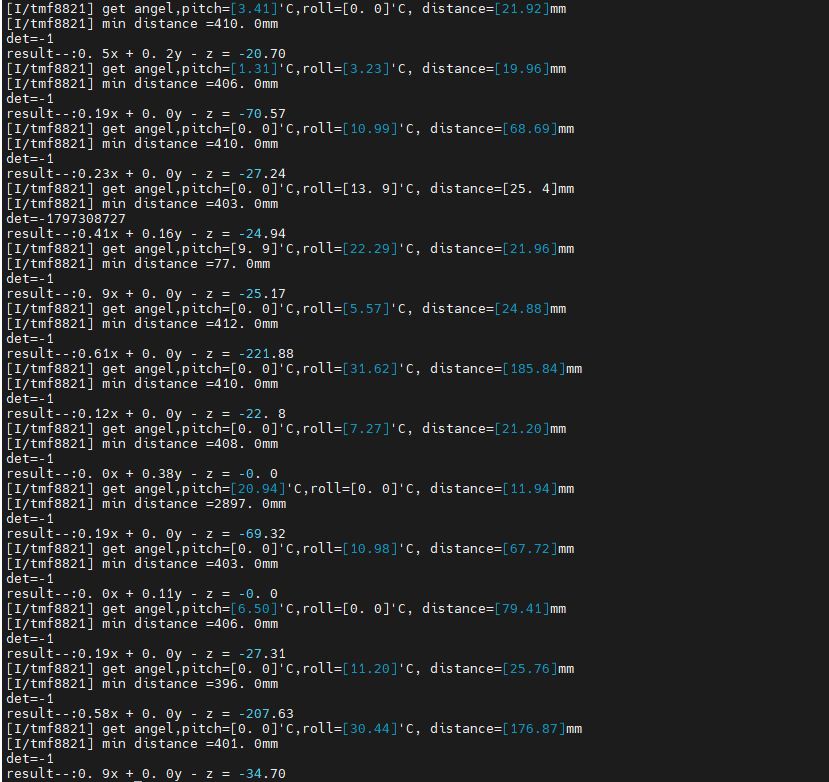

心得体会

目前的角度计算做的效果还很不理想，暂时猜测是没有引入滤波和置信度比例，需要再去测试修正。
dToF很强大，第一次用这么高级的传感器，希望多多发掘他的用途。
英文手册看的很吃力，要是没有群里大佬的教程可能早就放弃了。
这次活动认识到了自己的很多不足，给自己敲响了警钟，要补上这些不足。
感谢赞助商和硬禾带给我们这么好的活动。